0x00 基础算法与数据结构#

Talk is cheap. Show me the code.

—Linus Torvalds

图 12 Fibonacci spiral
Romain, CC BY-SA 4.0
via Wikimedia Commons#

斐波那契序列（Fibonacci sqeuence）

斐波那契序列的定义是：\(F_0 = 0, F_1 = 1, F_n = F_{n-1} + F_{n-2} (n \geq 2)\).

输入：: 一个非负整数 \(n\). 限定 \(n \in [0, 30]\).
输出：: 斐波那契序列的第 \(n\) 项（非前 \(n\) 项）。

重要

看似简单问题的背后，也可能蕴含着深刻的思想，所谓大道至简，正是如此。

备注

这一章主要通过一些基础的算法和数据结构，来介绍算法设计与分析的基本思想。假定读者已经了解了基本的编程语言知识，比如：变量、函数、循环、条件判断等，能够看懂伪代码。

算法设计的基本要素#

所谓算法，即特定计算模型 ¹ ¹💡 计算模型是指抽象出来的计算机或者计算过程的数学模型。常见的计算模型包括：有限状态自动机、图灵机、RAM机、并行计算模型等，其中 RAM 机（Random Access Machine）是最常用的计算模型，即一台具有随机访问存储器的机器，其指令集包含一组基本操作，每条指令都可以在常数时间内执行。下，旨在解决特定问题的指令序列。

输入：待处理的信息（问题）
输出：经处理的信息（答案）
正确性：的确可以解决指定的问题
确定性：可描述为一个由基本操作组成的序列
可行性：每一基本操作都可实现，且在常数时间内完成

²⚠️ 一些算法的有穷性难以证明，比如：停机问题, 科拉茨猜想等。

有穷性 ² ²⚠️ 一些算法的有穷性难以证明，比如：停机问题, 科拉茨猜想等。：对于任何输入，经有穷次基本操作，都可以得到输出

在计算模型满足基本条件，已给定输入输出时，我们关注算法正确性的证明：

逐条检验（Enumeration）emm… 仅推荐在问题规模极小时使用
数学归纳法（Mathematical Induction）
循环不变式（Loop Invariant）
反证法（Proof by Contradiction）… 等等

在一开始，不希望引入过多的严谨数学证明，而是希望通过一些简单的算法问题来建立起一种直观的认识。

理解迭代与递归#

迭代（Iteration）与递归（Recursion）是程序设计中的两类基本手段，它们都是通过反复调用某个子过程来达到求解问题的目的。为了能够看懂一些算法描述的伪代码（或实际的代码实现），我们需要能够充分理解这两种范式。通常它们之间可以互相转化，我们以斐波那契序列为例，来比较迭代与递归的区别。

迭代版

def fib_iteration(n):
    fib = [0, 1]
    for i in range(2, n+1):
        fib.append(fib[i-1] + fib[i-2])
    return fib[n]
        
fib_iteration(4)

迭代版的代码非常直观，可以通过下方的可视化代码来理解其执行过程。

递归版

Find the nth Fibonacci number — 图 13 递归跟踪
via THUDSA [11] 插图
对源文件有修改#

def fib_recursion(n):
    if n <= 1:
        return n
    return fib_recursion(n-1) + \
        fib_recursion(n-2)
        
fib_recursion(4)

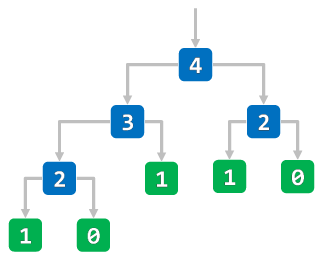
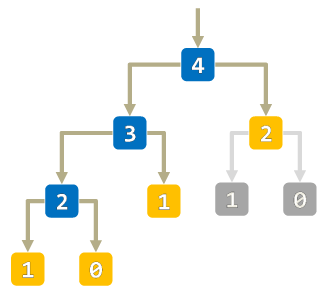
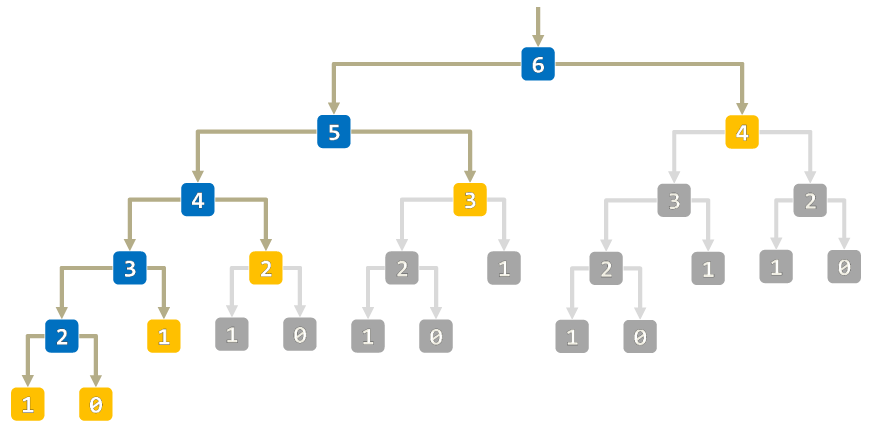
相较于迭代实现，递归实现的代码往往更加简洁，但容易出现多次重复调用的问题。注意下方演示代码中的函数栈调用过程，在程序递归过程中，每调用一次函数就会创建一个栈帧结构，而在每个栈帧结构中就会创建各自的局部变量，占用更多的内存空间。不难发现在递归调用的过程中出现了多次重复调用（可以通过记忆化的方式改善这一问题），试着将斐波那契序列的输入值改为 10，进一步观察两种实现方式的执行过程。

记忆化递归

Find the nth Fibonacci number (big) — 图 15 大规模输入
via THUDSA [11] 插图#

fib = [0, 1] + [None for _ in range(3)]

def fib_memoization(n):
    if fib[n] is None:
       fib[n] = fib_memoization(n-1) + \
            fib_memoization(n-2)
    return fib[n]
        
fib_memoization(4)

通过使用 记忆化（Memoization） 技术，我们可以有效地减少重复调用的次数，从而提高程序的执行效率。因此要写好一个递归程序，并没有那么简单，需要考虑到递归调用的次数、递归调用的深度限制，以及如何优化。

Wikipedia LeetCode 509 ³ ³💡 本 Wiki 中的参考代码下方通常会给出一些拓展材料和 Online Judge 平台的例题链接，供读者自行探索。

递归经典问题：汉诺塔#

通过斐波那契数列的例子，我们应该能够对递归函数的调用过程有一个基本的了解（更深层次的了解可能需要阅读汇编程序）。任何递归程序，都能够通过模拟函数调用栈的形式，来改为非递归的的写法，例如汉诺塔问题：

汉诺塔问题（Tower of Hanoi Problem）

有三根杆子 A，B，C. 在 A 杆上有 N 个 (N > 1) 穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 B 杆：每次只能移动一个圆盘；大盘不能叠在小盘上面。

输入：: 一个非负整数 \(n\). 限定 \(n \in [0, 30]\).
输出：: 满足最少移动次数的移动策略，每次移动输出一行如 “A -> B”

阅读 Wikipedia 中的介绍，递归解法原理如下，我们可以将解决过程其分解为三个子步骤：

将 \(n-1\) 个盘子从初始柱移动到辅助柱；
将最大的第 \(n\) 个盘子从初始柱移动到目标柱；
将 \(n-1\) 个盘子从辅助柱移动到目标柱。

递归性质：我们可以使用相同的逻辑来解决 \(n-1\) 个盘子的汉诺塔问题；
基本情况：当问题规模减少到只有一个盘子，即 \(n = 1\) 时，可以直接将该盘子从初始柱移动到目标柱。

递归版

void hanoi(int n, char source, char target, char helper) {
  if (n == 1) {
    printf("%c -> %c\n", source, target);
  } else {
    hanoi(n - 1, source, helper, target);
    hanoi(1,     source, target, helper);
    hanoi(n - 1, helper, target, source);
  }
}

可视化函数调用

迭代版（模拟函数调用）

例程来自蒋炎岩的操作系统课程，注意这是 C 语言实现。如果使用 C++ 语言，可以直接使用 std::stack 来作为栈容器，但无法体现底层原理。初学者无法理解下面代码的行为的话，也不用担心，可以当作补充知识。

typedef struct {
  int pc, n;
  char source, target, helper;
} Frame;

#define call(...) ({ *(++top) = (Frame) { .pc = 0, __VA_ARGS__ }; })
#define ret()     ({ top--; })
#define goto(loc) ({ f->pc = (loc) - 1; })

void hanoi(int n, char source, char target, char helper) {
  Frame stk[64], *top = stk - 1;
  call(n, source, target, helper);
  for (Frame *f; (f = top) >= stk; f->pc++) {
    n = f->n; source = f->source; target = f->target; helper = f->helper;
    switch (f->pc) {
      case 0: if (n == 1) { printf("%c -> %c\n", source, target); goto(4); } break;
      case 1: call(n - 1, source, helper, target); break;
      case 2: call(    1, source, target, helper); break;
      case 3: call(n - 1, helper, target, source); break;
      case 4: ret();                               break;
      default: assert(0);
    }
  }
}

本质上，这就是在模拟解释执行对应的汇编语句，手动维护函数调用栈帧（就像编译器所做的事情一样）。

算法分析的基本要素#

通过同一问题的不同算法（实现）进行分析，我们可以深入了解它们的优缺点和适用范围。这可以帮助我们更好地理解算法的原理和实现细节，并选择最适合我们需要的算法。在算法分析时通常不考虑机器的硬件和软件环境差异，也不考虑算法所用编程语言的特性差异，主要关注：

时间复杂度：算法的运行时间与问题规模之间的增长关系
空间复杂度：算法的存储空间与问题规模之间的增长关系

时间复杂度#

算法的时间复杂度是定义域在自然数集合的函数，它表示算法的运行时间与问题规模之间的增长关系。记当前算法的输入规模为 \(n\)，算法的执行时间成本 ⁴ ⁴💡 时间成本~各条指令执行次数之总和为 \(T(n)\). 有 Big Oh 与 Small Oh 两类渐近记号：

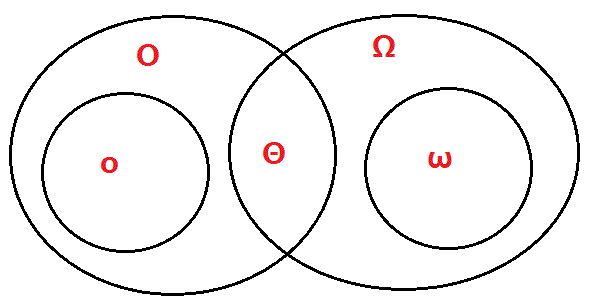
Time complexity notation set — 图 17 渐近记号之间的关系#

Big Oh

对于大规模问题，考虑以渐近意义上的时间复杂度表示 \(T(n)\) 的增长趋势。使用 \(\epsilon - N\) 表示法，则有：

\(T(n) \in O(f(n))\): 存在正数 \(C\) 和 \(n_0\)，使得当 \(n \geq n_0\) 时，有 \(T(n) \leq C f(n)\).
\(T(n) \in \Omega(f(n))\): 存在正数 \(C\) 和 \(n_0\)，使得当 \(n \geq n_0\) 时，有 \(T(n) \geq C f(n)\).
\(T(n) \in \Theta(f(n))\): 存在正数 \(C_1, C_2\) 和 \(n_0\)，使得当 \(n \geq n_0\) 时，有 \(C_1 f(n) \leq T(n) \leq C_2 f(n)\).

其中，\(O(f(n))\) 表示渐进上界，\(\Omega(f(n))\) 表示渐进下界，\(\Theta(f(n))\) 表示渐进紧确界。

使用极限的语言来描述（注意极限不一定存在），即：

\(T(n) \in O(f(n))\): \(\lim_{n \to \infty} \frac{T(n)}{f(n)} = C < \infty\).
\(T(n) \in \Omega(f(n))\): \(\lim_{n \to \infty} \frac{T(n)}{f(n)} = C > 0\).
\(T(n) \in \Theta(f(n))\): \(\lim_{n \to \infty} \frac{T(n)}{f(n)} = C \in (0, \infty)\).

Small Oh

如果去掉等号，则得到了算法的非渐进紧确界。使用 \(\epsilon - N\) 表示法，则有：

\(T(n) \in o(f(n))\): 对于任意正数 \(C\)，存在正数 \(n_0\)，使得当 \(n \geq n_0\) 时，有 \(T(n) < C f(n)\).
\(T(n) \in \omega(f(n))\): 对于任意正数 \(C\)，存在正数 \(n_0\)，使得当 \(n \geq n_0\) 时，有 \(T(n) > C f(n)\).

其中，\(o(f(n))\) 表示算法的非渐进紧确上界，\(\omega(f(n))\) 表示算法的非渐进紧确下界。

使用极限的语言来描述，则类似于无穷比阶，即：

\(T(n) \in o(f(n))\): \(\lim_{n \to \infty} \frac{T(n)}{f(n)} = 0\).
\(T(n) \in \omega(f(n))\): \(\lim_{n \to \infty} \frac{T(n)}{f(n)} = \infty\).

通常我们所指的算法复杂度，即 \(O(f(n))\)，常用性质如下：

忽略常系数：\(O(f(n)) = O(c \cdot f(n))\)
高阶吸收低阶：\(O(n^a + n^b) = O(n^{\max(a, b)})\)

上面的性质可以帮助我们快速整理简化算法的复杂度，抓住重点，返璞归真。

空间复杂度#

算法的空间复杂度指的是算法在执行过程中额外所需要的存储空间大小。也就是说，空间复杂度描述的是算法对内存的需求程度，包括程序代码本身所占用的空间以及算法执行时所需要的额外空间。

通常情况下，空间复杂度可以用一个简单的表达式来表示，该表达式与算法的输入规模有关。例如，当输入规模为 \(n\) 时，一个算法的空间复杂度可能是 \(O(1)\), \(O(n)\), \(O(n^2)\) 等。在算法设计和优化过程中，空间复杂度也是一个重要的指标。较低的空间复杂度可以提高算法的效率和性能，减少计算机内存的使用量。同时，也可以使算法更加节省成本，降低运行成本。在实际应用中，我们需要根据具体情况选择合适的算法，平衡时间复杂度和空间复杂度之间的关系，以便在资源受限的环境中获得最佳性能。

随着现代存储技术的发展，计算机的存储空间越来越大，因此空间复杂度的重要性也越来越低。我们在设计算法时，通常更加关注时间复杂度上的优化。但是对于一些特殊的应用场景（例如嵌入式系统、移动设备、大参数模型等资源受限的环境），空间复杂度仍然是一个重要的考量因素。

小技巧

想一想，求斐波那契序列的第 \(n\) 项，是否存在空间复杂度为 \(O(1)\) 的算法？

我们在下一小节将介绍可能的做法，请你不妨先自己想一想。

空间换时间#

警告

查询次数也应当被视作是算法的输入规模之一，即问题规模的一部分。

由于我们更加看重算法的时间复杂度，因此在实际应用中，我们通常会通过适当地增加空间复杂度来降低时间复杂度，这种做法被称为 空间换时间，也叫 ”打表“。求解斐波那契序列虽然存在着空间复杂度为 \(O(1)\) 的算法，但每次都需从头计算，只适用于单次查询；如果需要 多次查询（Multiple queries），那么空间复杂度为 \(O(n)\) 的迭代算法将更加适用。因为我们很容易就能发现，在计算第 \(n\) 项斐波那契数的过程中，前面的 \(n-1\) 项斐波那契数都已经计算出来了，因此我们可以将这些斐波那契数缓存起来，后续查询时间复杂度仅为 \(O(1)\).

接下来我们将介绍两类经典问题和对应的算法，用到了空间换时间的思想。

构造累积数组#

区间求和问题（Interval summation problem）

输入：: 一个长度为 \(n\) 的整数序列 \(A\), 以及 \(m\) 个查询，每个查询包含两个整数 \(l\) 和 \(r\).
输出：: 每次查询区间内元素 \(A[l], A[l+1], \cdots, A[r]\) 的和。（保证不会出现溢出）

暴力解（Brute-force）

对于每个查询，都遍历一遍区间内的元素，计算它们的和。这样做的空间复杂度为 \(O(1)\) (仅需额外存储当前查询的区间和)。但总的时间复杂度为 \(O(nm)\)，显然无法接受。

小技巧

不难发现这样一个性质：即对于任意的 \(l\) 和 \(r\)，区间 \([l, r]\) 的和可以表示为 \([0, r]\) 的和减去 \([0, l-1]\) 的和。因此在遍历序列中的每个元素时，我们可以同时计算出 \([0, i]\) 的和（前缀和），以便后续的查询。

构造：\(\operatorname{prefixSum}[i] = A[0] + A[1] + ... + A[i]\)
则有：\(\operatorname{intervalSum}[l, r] = \operatorname{prefixSum}[r] - \operatorname{prefixSum}[l-1]\)

额外所需的空间复杂度为 \(O(n)\)，构造累积数组的时间复杂度为 \(O(n)\)，每次查询的时间复杂度为 \(O(1)\)，总的时间复杂度为 \(O(n + m)\).

Wikipedia LeetCode 1480 LeetCode 303 LeetCode 307 LeetCode 53 AcWing 795 AcWing 796

构造差分数组#

区间修改问题（Interval modification problem）

输入：: 一个长度为 \(n\) 的整数序列 \(A\), 以及 \(m\) 个操作，每次操作包含三个整数 \(l, r, c\).
输出：: 对于每个操作，将区间 \([l, r]\) 内的所有元素加上 \(c\). 最后输出整个序列 \(A\). （保证不会出现溢出）

暴力解（Brute-force）

对于每次操作，都遍历一遍区间内的元素，将它们加上 \(c\). 时间复杂度为 \(O(nm)\)，显然无法接受。

小技巧

由于对区间的修改是 连续且一致 的，因此可以思考能否只对修改的起点和终点位置做一次特殊记录，希望以“牵一发而动全身”的形式来体现整体的改动，即前缀中的任何改动都会对当前位置产生影响。我们可以只记录相邻元素之间的差值，即差分数组。则任何位置都可以通过另一位置不断累积差分得到。

构造：\(\operatorname{diff}[i] = A[i] - A[i-1]\)
则有：\(A[i] = \operatorname{diff}[0] + \operatorname{diff}[1] + ... + \operatorname{diff}[i]\)

额外所需的空间复杂度为 \(O(n)\)，构造差分数组的时间复杂度为 \(O(n)\)，每次操作的时间复杂度为 \(O(1)\)，总的时间复杂度为 \(O(n + m)\).

Wikipedia LeetCode 1109 AcWing 797 AcWing 798

空间局限性#

空间换时间的思想通常涉及到通过预处理和存储一些中间结果或者其他有用的信息，以减少算法执行时的计算量。但并不是所有的问题都适合这种思想，尤其是在有穷性无法得到保证的情况下，这种思想可能会导致算法不可行。例如，如果我们需要计算三角函数的值，虽说总可以通过预先计算并存储一些常用的值来减少计算量。但我们无法完全穷举出所有可能的取值，本质上是定义域为实数域 \(\mathbb R\), 而实数域即使在区间 \([0, 1]\) 也是无穷的。再比如，我们将区间求和问题的索引范围扩大到整个数轴（而非在有限长度序列上操作），此时则无法直接使用前缀和的思想来解决问题，因为此时我们无法预先计算并存储所有的可能。

另外，即使输入规模有穷，空间换时间的思想也可能导致空间复杂度过高的问题出现。例如，如果我们需要计算一个整数序列中的指定子序列的和，虽然的确可以通过预处理并存储所有结果来实现 \(O(1)\) 的查询。但采取这样的做法，我们将需要额外的 \(O(2^n)\) 的空间来存储所有的可能，这显然是不可接受的（且时间复杂度也很高）。

这有些画蛇添足的味道，实际上这个问题解法异常简单，我们只需要存储原始序列，并在查询时即时计算即可。

从内存视角理解程序#

警告

每个程序设计人员都有必要了解计算机系统及语言提供的的内存管理（Memory management）机制。

这一部分的内容虽然和算法的设计思想没有直接的关系，但却是算法设计的一个重要的考虑因素。另外它也会深刻地影响我们的代码风格，以及代码的可维护性。如果不理解有关知识，我们将无法分辨什么是好的代码，什么是坏的代码，什么是可维护的代码，什么是不可维护的代码。对于一些未曾有过算法竞赛经验，但参与工程开发很久的人员而言，阅读一份竞赛选手的代码可能会感到非常困惑，里面充斥着各种奇怪的写法，这些写法在工程开发中是不被允许的，但在算法竞赛中却是常见的。这是因为这些算法竞赛中的代码（以及代码模板）通常是为了追求速度（包括编码速度和运行时速度）而牺牲了可读性和可维护性，通常具有极强的个人风格与学习成本。

例如我们后面将要介绍的链表、栈、队列等数据结构，在打比赛时我们通常会使用静态数组来模拟实现，而不是使用 C++ STL 中的 std::list, std::stack, std::queue 等容器。这是因为 STL 容器的实现通常是基于动态内存分配的，而动态内存分配的效率很低，且容易出现内存泄漏的问题；另外如果编译器如果没有开 O2 优化，那么 STL 容器的效率会更低。但作为工程开发人员，我们通常会使用 STL 容器，因为它们的使用非常方便，且不需要我们关心内存管理的问题。因此，我们需要在不同的场景下适配代码风格，这就要求掌握各种写法。

以双向链表为例#

重要

如果你还不知道什么是链表，可提前参考 0x04 数组与链表（列表）章节。

设计双向链表（Doubly linked list）

现要求实现一个双向链表，支持 5 种操作：

在最左侧插入一个数；
在最右侧插入一个数；
将第 \(k\) 个插入的数删除；
在第 \(k\) 个插入的数左侧插入一个数；
在第 \(k\) 个插入的数右侧插入一个数。

注意：题目中第 \(k\) 个插入的数并不是指当前链表的第 \(k\) 个数。

Wiki AcWing 827

动态双链表

如果老老实实地去实现一个满足题目要求的数据结构，代码可能是这样的：

注意为了简化讨论，使用了 dummy 头尾节点，真正的头尾节点分别位于 header->next 和 tailer>prev.
为了实现第 3 个操作，我们需要维护一个数组 kth，其中 kth[i] 表示第 i 个插入的数对应的节点指针；
由于内存的申请和释放主要通过 new 和 delete 实现，因此这种链表的类型是动态的。

struct node {
    int val;
    node* prev;
    node* next;

    node(int e = 0, node* p = nullptr, node* n =nullptr) 
        : val(e), prev(p), next(n) {}
};

struct list {
    node* header;
    node* tailer;
    node dummy_head, dummy_tail;

    vector<node*> kth;  // specified for this problem

    void init() {
        header = &dummy_head;
        tailer = &dummy_tail;
        header->next = tailer;
        tailer->prev = header;

        kth.clear();
        kth.push_back(header);
    }

    list() { init(); }

    void insertAtRight(int val, int idx) {
        node* p = kth[idx];
        node* x = new node(val, p, p->next);
        p->next->prev = x;
        p->next = x;
        kth.push_back(x);
    }

    void insertAtLeft(int val, int idx) {
        node* p = kth[idx];
        node* x = new node(val, p->prev, p);
        p->prev->next = x;
        p->prev = x;
        kth.push_back(x);
    }

    void insertAtFirst(int val) {
        insertAtRight(val, 0);
    }

    void insertAtLast(int val) {
        node* x = new node(val, tailer->prev, tailer);
        tailer->prev->next = x;
        tailer->prev = x;
        kth.push_back(x);
    }

    void remove(int idx) {
        node* target = kth[idx];
        target->prev->next = target->next;
        target->next->prev = target->prev;
        delete target;
    }
};

实际上打比赛的时候很难像上面一样中规中矩地实现一个数据结构，而是直接用大数组来模拟。

我们不希望在链表操作的过程中出现太多的 new 和 delete 操作，在大规模测试用例下，这些操作的效率会很低。因此我们总是能够在内存空间足够的情况下，提前地去申请好一大块连续的内存（即大数组，也可称之为简易内存池），手动地在数组上模拟指针链表所拥有的操作。这就好像我们的电脑内存其实也是固定容量的，操作系统做的也无非是替用户维护管理内存的分配和使用（没有学过操作系统课程的读者请忽略这里的类比）。

这一大块内存的大小是固定的（但至少满足题目所需），无法缩减或扩容，因此也叫静态链表。

静态双链表

如果编程语言中没有提供指针这一概念，我们该如何实现双链表呢？

让我们借由额外的索引数组，建立起静态双链表与动态双链表之间的比对关系：

e[M] 对应 val, 即存放节点的值，意味着所有数据变成了静态连续存储，可通过下标定位；
l[M] 对应 prev, 即存放节点的前驱节点的下标；
r[M] 对应 next, 即存放节点的后继节点的下标；（在单链表中常命名为 ne 或 link）
head 对应 header, 即存放 dummy 头节点的下标，同理 tail 对应 tailer；
同样地，由于使用了 dummy 节点，真正的头节点在 r[head], 尾节点在 l[tail]；

初学者最大的疑惑可能是：之前学链表的时候讲了这么多指针的概念，这里的实现怎么连指针都没出现？！

替换 *: 使用下标值对指针进行抽象，如用 head 表示头指针，它的值是头节点在数组中的下标；
- 因此头节点的值为 e[head], 前驱节点的值为 e[l[head]], 后继节点的值为 e[r[head]]；
- 一定要深刻理解 使用下标索引来代替指针 的思想，这是理解任何静态数据结构的核心；
替换 new: 我们总是需要维护一个指针性质的变量（如 idx），在静态链表中它就是一个下标，指向当前可被分配使用的单位类型内存。插入新的节点时，直接维护 e[idx] 和 ne[idx], 再令 idx++.
替换 delete: 实际上并没有真的做删除，而是直接废弃/无视/跳过被删除节点，而指向它的下一个节点，不再有任何节点的下一个节点指针指向它，且这块空间在这个大数组中不会再被用到，因为 idx 永远只会递增。这很容易出现所谓的内存碎片，但是比赛时不需要担心这个问题。

这种实现方式也被称为链表的 游标实现，因为我们使用游动下标来代替指针。

const int M = 1e5 + 10;

int e[M], l[M], r[M];
int head, tail, idx;

// DUMMY_HEAD -> REAL_HEAD -> ... -> REAL_TAIL -> DUMMY_TAIL
// ^                                              ^
// HEAD_POS                                       TAIL_POS

#define HEAD_POS (0)
#define TAIL_POS (M-1)

void init() {
    head = HEAD_POS;
    tail = TAIL_POS;
    r[head] = tail;
    l[tail] = head;
    idx = 1;
}

void insert(int k, int x) {
    e[idx] = x;
    l[idx] = k;
    r[idx] = r[k];
    l[r[k]] = idx, r[k] = idx++;
}

void del(int k) {
    l[r[k]] = l[k];
    r[l[k]] = r[k];
}

5 种接口等价调用方式如下：

insert(HEAD_POS, x);
insert(l[TAIL_POS], x);
del(k);
insert(l[k], x);
insert(k, x);

所以在竞赛时使用数组来模拟数据结构的技巧，背后的原理其实和计算机科学某些课程中的原理是融会贯通的，关键点在于两个字：抽象，我们赋予了一些执行序列以特殊的意义，使得它们能够模拟出我们想要的数据结构的操作，问题在于这种抽象的建立是需要规范和约定的，因此理解起来需要一定的时间，理解成本也是比较高的。这也能与编程范式挂钩，你可以认为，动态链表的实现是面向对象思想的体现，而静态链表的实现是面向过程思想的体现，前者对行为进行了显式接口封装，后者更关注我们如何直接地修改数据，是隐晦的抽象。

观察静态链表的实现，你会发现我们可以对原始的动态链表实现进行一定的重构，使得它更加简洁。

动态双链表（重构）

可通过重构代码，实现更加强大的 insert 和 remove, 直接接受接受节点指针 p 从而进行定位。

struct node {
    int val;
    node* prev;
    node* next;

    node(int e = 0, node* p = nullptr, node* n =nullptr) 
        : val(e), prev(p), next(n) {}
};

struct list {
    node* header;
    node* tailer;
    node dummy_head, dummy_tail;

    vector<node*> kth;  // specified for this problem

    void init() {
        header = &dummy_head;
        tailer = &dummy_tail;
        header->next = tailer;
        tailer->prev = header;

        kth.clear();
        kth.push_back(header);
    }

    list() { init(); }

    void insert(node* p, int val) {
        node* x = new node(val, p, p->next);
        p->next->prev = x;
        p->next = x;
        kth.push_back(x);
    }

    void remove(node* p) {
        p->prev->next = p->next;
        p->next->prev = p->prev;
        delete p;
    }
};

5 种接口等价调用方式如下：

l.insert(l.header, x);
l.insert(l.tailer->prev, x);
l.remove(l.kth[k]);
l.insert(l.kth[k]->prev, x);
l.insert(l.kth[k], x);

看到这里，你应该发现不论是动态链表还是静态链表，它们都是对链表这一数据结构的逻辑采用了不同的物理实现，二者大道至简，殊途同归。

不要排斥使用 STL#

理想情况下，静态数据结构的代码写起来很快，效率也更高，但是这并不意味着你应该排斥使用 STL，因为：

STL 的实现是经过严格测试的，你不需要担心它的 Bug，而你自己实现的数据结构可能会有 Bug；
STL 的实现是经过优化的，你不需要担心它的效率，而你自己实现的数据结构可能会有效率问题；
在实现一些复杂的数据结构时，你可能会发现 STL 的实现比你自己实现的更加简洁，更加优雅，更加高效。

而要达到所谓的理想情况，前提是你必须将各种静态数据结构的写法熟稔于心，对底层细节了解充分，这样你才能够在比赛时快速地写出正确的代码。而在学习某一种数据结构时，我依旧推荐先从基于 STL 的实现开始，因为这样你可以更快地理解这种数据结构的逻辑，而不是被一些细节所困扰。有的时候，慢即是块。当你充分掌握一种数据结构的逻辑后，则可以尝试自己实现一遍动态/静态版本，这样你才能够更加深入地理解这种数据结构。

STL 也有一定的缺陷，比如一些代码可能导致未定义行为（Undefined Behavior）产生，而如果你不清楚编译器对未定义行为的实现差异，形成了一些思维定势，那么你的代码可能会出现一些奇怪的 Bug.

参见

在后面介绍的数据结构的章节中，我们通常会额外提供一份使用 STL 接口实现的高效数据结构。区别在于，我们假定读者已经了解内存相关的知识，不再将懂得设计内存分配器作为前提。

0x00 基础算法与数据结构

目录

0x00 基础算法与数据结构#

算法设计的基本要素#

理解迭代与递归#

递归经典问题：汉诺塔#

算法分析的基本要素#

时间复杂度#

空间复杂度#

空间换时间#

构造累积数组#

构造差分数组#

空间局限性#

从内存视角理解程序#

以双向链表为例#

不要排斥使用 STL#