0x01 排序算法与思想#

Premature optimization is the root of all evil.

—Donald Knuth

排序问题（Sorting problem）

输入：

由 \(n\) 个数字组成的序列 \(\left\langle a_1, a_2, \ldots, a_n\right\rangle\).

输出：

重新排序后的序列 \(\left\langle a_1^{\prime}, a_2^{\prime}, \ldots, a_n^{\prime}\right\rangle\), 使得 \(a_1^{\prime} \leq a_2^{\prime} \leq \cdots \leq a_n^{\prime}\).

注意

当一个整数数组 \(A\) 被排序后，许多涉及到 \(A\) 的问题会变得容易（或更容易）： 例如在数组 \(A\) 中查找特定值 \(v\), 找到静态数组 \(A\) 的最小/最大值或第 \(k\) 大/小的值， 测试数组 \(A\) 中是否有重复值并删除重复值， 计算特定值 \(v\) 在数组 \(A\) 中出现的次数， 对数组 \(A\) 和另一个已排序的数组 \(B\) 进行集合交/并操作， 找到目标值对 \(x \in A\) 和 \(y \in A\), 使得 \(x+y\) 等于目标值 \(z\), 计算数组 \(A\) 中有多少个值位于区间 \([lo..hi]\) 中等等… 前提是原问题的最优解复杂度 不低于 所采用的排序算法的复杂度。

设计排序算法时，考虑初始序列各种可能的状态

  • 不含有重复元素，含有少量重复元素，含有大量重复元素，全部重复元素；

  • 逆序序列，部分逆序序列，完全有序序列；

  • 元素值的大小范围，元素值的分布情况；

  • 序列长度，序列的存储结构 … 等等，同一算法的复杂度可能会随着这些因素的变化而变化。

Zero indexing 与开闭区间取舍

如果你习惯使用 C++ STL 接口，则自然习惯于使用左闭右开区间 \([low, high)\), 亦或者写成 \([first, last)\). 对于 Zero-based indexing 的语言，如 C/C++/Java/Python 等，这种习惯是合理的。

stl::vector<int> v;
stl::sort(v.begin(), v.end());

但有的时候我们也会使用左闭右闭区间，比如本章节的排序算法，这种定义写起来方便记忆。 只是在调用的时候，注意与 STL 接口的区别（通常用 \([left, right]\) 表示都是闭区间）：

void mySort(vector<int> &array, int left, int right) {
    // ...
}

mySort(v, v.begin(), v.end() - 1);

冒泡排序#

让我们从最容易理解的排序算法开始：冒泡排序（Bubble sort）。 我们将借此来初步理解算法设计的经典策略，减治法（Decrease-and-Conquer），或称之为减而治之。 顾名思义，为求解一个大规模的问题，将其划分为两个子问题： 其一平凡（trivial，即不需要进行复杂处理的子问题），另一规模缩减（满足单调性）， 然后迭代地解决平凡的子问题（或递归地求解），最终可由子问题的解，组合得到原问题的解。

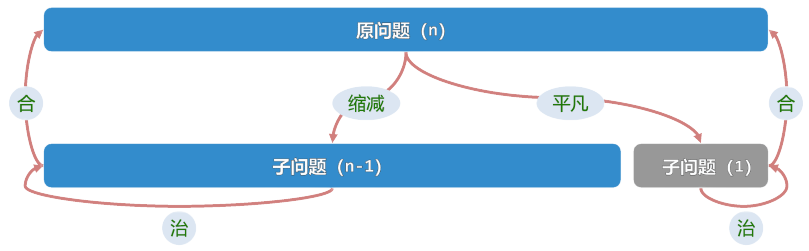
Decrease-and-conquer

图 1 减而治之 （ via THUDSA [11] 配套讲义，对源文件有修改）#

不难发现，倘若我们能够 每次都找出当前序列中的最大值，然后将其放置在序列的最后位置， 那么问题的规模就得以减少，假定原问题规模为 \(n\)，那么剩余子问题规模为 \(n-1\)，如此迭代至多 \(n\) 次即可得到原问题的解。

减而治之：发现平凡子问题#

最大值放置问题

输入：

由 \(n\) 个数字组成的序列 \(\left\langle a_1, a_2, \ldots, a_n\right\rangle\).

输出：

找出其中的最大值 \(a_{\max}\), 并将其放置在序列的最后。

Bubble sort

图 2 Bubble sort
Swfung8, CC BY-SA 3.0
via Wikimedia Commons#

冒泡排序即解决上述平凡子问题的一种策略，基本思想是： 从数组的第一个元素开始，通过相邻元素之间的比较，不断交换相邻元素的位置，确保较大的元素在后面， 最终当前序列中最大的元素将被放置在最后的位置。平凡问题得解。

为何称之为冒泡排序呢？因为将序列中的元素看作一个个气泡的话，从最底下的气泡开始“往上冒”， 相邻气泡比较时，较大的气泡将会更容易浮在上面，直到遇到水面（最后的位置）。

代码实现如下，输入序列 array, 对其闭区间 [left, right] 上的元素进行冒泡排序：

void bubble_sort(vector<int> &array, int left, int right) {
    if (left>= right) return;  // only one element left

    for (int j = left; j < right; ++j) {  // a trivial subproblem
        if (array[j] > array[j + 1]) {
            swap(array[j], array[j + 1]);
        }
    }
    
    bubble_sort(array, left, right-1);  // decrease-and-conquer
}

上面的代码使用递归（Recursion）的方式实现了冒泡排序，这种写法能够更直观地看出减而治之的过程。 递归的终止条件很明显，当问题规模减少到只有一个元素时，无需进行任何处理，直接返回即可。

下面是迭代（Iteration）实现，通过明确循环范围来控制何时停止，对大部分人而言更为常见：

void bubble_sort(vector<int> &array, int left, int right) {
    for (int i = left; i < right; ++i) {  // decrease-and-conquer
        for (int j = left; j < right - i; ++j) {  // a trivial subproblem
            if (array[j] > array[j + 1]) {
                swap(array[j], array[j + 1]);
            }
        }
    }
}

简单进行一下复杂度分析：外层循环迭代 \(n-1\) 次，内层循环迭代 \(n-1, n-2, \cdots, 1\) 次， 总的比较次数为 \(\sum_{i=1}^{n-1} i \ = 1 + 2 + \cdots + n-1 \ = \frac{n(n-1)}{2}\)， 因此时间复杂度为 \(O(n^2)\).

原始版本的冒泡排序有着明显的缺点，即使序列已经有序（包括在某一轮冒泡后序列达到有序）， 当前的实现仍然需要总共进行 \(n-1\) 轮比较，这是不必要的。 因此一种优化思路是：在每一轮冒泡中，若没有发生交换，则说明序列已经有序，无需再进行后续的冒泡。 （可切换到 “提前终止” 标签进行了解）

  • 我们使用了一个布尔变量 swapped 来标记当前轮次是否发生了交换；

  • 若没有发生交换，则说明序列已经有序，无需再进行后续的冒泡。

void bubble_sort(vector<int> &array, int left, int right) {
    for (int i = left; i < right; ++i) {  // decrease-and-conquer
        bool swapped = false;
        for (int j = left; j < right - i; ++j) {
            if (array[j] > array[j + 1]) {
                swap(array[j], array[j + 1]);
                swapped = true;
            }
        }
        if (!swapped) break;
    }
}

在初始序列接近有序甚至完全有序的情况下， 此时冒泡排序的时间复杂度将会降低到 \(O(n)\). 但对于大规模的随机序列输入，在平均情况下，时间复杂度依然为 \(O(n^2)\). 不难得出结论，该版本的冒泡排序的确在特定情况下能够优化程序性能，但总的收益并不明显。

双向冒泡排序又叫鸡尾酒排序、来回排序，其基本思想是：

  • 我们使用两个指针 left 和 right 分别指向当前序列的左右边界；

  • 每一轮冒泡，我们分别从左向右和从右向左进行一次冒泡，直到两个指针相遇。

void bubble_sort(vector<int> &array, int left, int right) {
    while (left < right) {
        
        bool swapped = false;
        for (int i = left; i < right; ++i) {
            if (array[i] > array[i + 1]) {
                swap(array[i], array[i + 1]);
                swapped = true;
            }
        }
        if (!swapped) break;
        --right;

        swapped = false;
        for (int i = right; i > left; --i) {
            if (array[i] < array[i - 1]) {
                swap(array[i], array[i - 1]);
                swapped = true;
            }
        }
        if (!swapped) break;
        ++left;
    }
}
💡 相较于单向冒泡，双向冒泡排序的优势

不妨思考一下，双向冒泡排序相较于单向冒泡的提前终止版本，做出了哪些改进？试输入如下序列：

\[ [1, 2, 3, 4, 5, 6, 7, 8, 9, 0] \]

我们能否认为它是一个接近有序的序列？如果是，那么提前终止的冒泡排序的时间复杂度将会降低到 \(O(n)\). 但模拟一下排序过程你就会发现，末尾元素的冒泡需要经过 \(n-1\) 轮，因此时间复杂度依然为 \(O(n^2)\). 在这个过程中，每一轮冒泡都发生了一次交换行为，因此提前终止的优化策略并没有发挥作用。

如果我们以任意元素距离其最终理想位置的距离最大值作为序列有序程度的度量标准，那么上述序列的有序程度接近 \(n\). 最关键点在于：单向冒泡排序中，对于每一轮冒泡，当前的非最大元素（如上面的 0）至多只能借助交换的形式向理想位置移动一步， 而只有最大元素能够在此轮冒泡不断交换至最末的位置。

双向冒泡排序等于补足了单向冒泡排序在冒泡方向考虑的不足，使得每一轮冒泡中，当前方向上的极端元素都能够直接移动到理想位置。 可以得出结论，双向冒泡能够使 含少量非理想位置元素 的初始序列能够更快地达到有序状态，使得提前终止策略能够真正地发挥作用。

Wikipedia Visualgo LeetCode 912

警告

冒泡排序相当低效（包括与其它 \(O(n^2)\) 级别排序算法相比），因此在绝大部分场景下都不提倡使用。 在教学排序算法时，一些教科书也不再选择介绍冒泡排序，而是从选择排序或插入排序开始。

⌛ Time Limit Exceeded (TLE)

借助冒泡排序算法，我们成功地实现了对随机序列的排序。但如果将冒泡排序算法提交到 LeetCode 等评测平台上，你会发现它的运行时间远远超过了其他排序算法。 而且我们会得到一个 Time Limit Exceeded 的错误提示，这意味着我们的程序运行时间超过了 LeetCode 的限制。 在 LeetCode 上的排序题目，包括冒泡排序在内的大部分 \(O(n^2)\) 级别排序算法都会超时。

参见

想要找到容器中的最大/最小元素位置，可以使用 std::max_element 和 std::min_element 函数。

选择排序#

在冒泡排序中，出现了太多次的交换（Exchange）操作，这是导致程序运行时间过长的主要原因之一。

自然地，我们有了一个优化算法的思考方向：如何将交换的次数减少？

让我们回归到减而治之思想，考虑排序问题的平凡子问题描述：将当前序列的最大元素移动到最后。 为了遵循约定俗成的习惯，后面我们换用等价表述：将当前序列的最小元素移动到最前。

减而治之：寻找高效治理策略#

Selection sort

图 3 Selection sort
Suaudeau, CC BY-SA 4.0
via Wikimedia Commons#

比对整个序列的初始状态和最终状态，似乎未必需要通过多轮交换来达成上述目的。 我们可以通过一次遍历，找到当前序列的最小元素，然后选择其与当前序列的第一个元素交换。 采用这种思路的算法被称为 选择排序（Selection sort） 。 同样地，选择排序体现了减而治之思想，只是对等价平凡子问题的解法更加高效。

void selection_sort(vector<int> &array, int left, int right) {
    for (int i = left; i < right; ++i) {  // decrease-and-conquer
        int min_index = i;
        for (int j = i + 1; j <= right; ++j) {
            if (array[j] < array[min_index]) {
                min_index = j;
            }
        }
        swap(array[i], array[min_index]);
    }
}

void selection_sort(vector<int> &array, int left, int right) {
    if (left >= right) return;  // only one element left

    int min_index = left;
    for (int j = left + 1; j <= right; ++j) {
        if (array[j] < array[min_index]) {
            min_index = j;
        }
    }
    swap(array[left], array[min_index]);

    selection_sort(array, left + 1, right);  // decrease-and-conquer
}

Wikipedia Visualgo LeetCode 912

选择排序的性能分析

相较于冒泡排序，当发现更小的元素时，选择排序不会立即交换，而是记住该元素的位置。 接着继续遍历整个序列，最终将找到最小元素的位置，并基于此位置进行一次交换。

在比较的次数相同的情况下， 发生交换的次数更少（共 \(n-1\) 次），因此指令执行次数也更少，这是一种 常数级别的优化。 但是选择排序时间复杂度仍取决于比较的次数（且不存在提前终止的情况）， 依旧为 \(O(n^2)\), 与原始版冒泡排序改进为双向冒泡相同，常数优化不能带来理论时间复杂度的改进。

❓ 提前终止的双向冒泡排序更优吗

我们不能够因为冒泡排序能够提前终止而认为其优于选择排序。 提前终止的前提条件十分严苛，即数组已然有序。 在输入序列是随机分布的情况下，考虑其发生概率，可以看作这一前提是不成立的。 我们在比较算法的优劣时，应该考虑最坏情况下的时间复杂度。 不考虑常数意义，冒泡排序和选择排序半斤八两。

❓ 进行常数意义下的优化有意义吗

我们在分析算法的时间复杂度时，通常不考虑常数意义上的优化。 这是因为常数级别的优化，往往需要付出更多的代价，比如破坏代码的可读性、可维护性等。 在实际工程的常见情景中，我们更加关注代码的可维护性，而不是一味地追求性能。 Donald Knuth 在《计算机程序设计艺术 [6] 》中提到，程序员的时间比机器的时间更加宝贵。 同时有一句关于优化的名言：过早优化是万恶之源。

但是事无绝对，在高性能计算等等领域，常数级别的优化是十分重要的。 在这些领域，我们需要考虑的是算法的实际执行时间，而不是时间复杂度。 同时还要考虑算法的空间复杂度，因为此时内存访问的代价是十分昂贵的。 甚至乎还需要考虑连续内存读写和随机内存读写的代价，因为此时 CPU 缓存的命中率是十分重要的。 这些讨论已经涉及到了计算机体系结构的知识，超出了本 Wiki 关注的重点。

假定我们的计算模型存在这样的缺陷：交换操作指令的开销高出写入操作至少一个数量级（脱离常数级别）， 那么在这种假定条件下，选择排序的性能将优于冒泡排序。 所以算法设计不能一概而论，只是通常为了简化讨论，我们认为计算模型是一台标准 RAM 机器， 不考虑 ISA 和硬件设计带来的影响。

在算法竞赛时，一些古怪的题目可能会卡常数，这时候我们需要考虑常数意义上的优化。😅

小技巧

冒泡排序和选择排序都采取了减而治之的策略，将大规模的原问题分解出平凡子问题， 在求解每个平凡子问题的过程中，通过缩小问题规模来逐步得到大问题的部分解，最终合并。 试着换一种思考的角度，如果原问题的解可以看作是由平凡问题的解经过多次递推得到呢？

插入排序#

插入问题

输入：

一个有序序列 \(\left\langle a_1, a_2, \ldots, a_n\right\rangle\) 与一个元素 \(x\).

输出：

将 \(x\) 插入到序列中，使得新序列仍然有序.

倘若已知 \(A[1,i]\) 序列有序，现在要将一个新元素 \(a_{i+1}\) 插入到这个已排序的序列中， 那么我们只需要从 \(a_i\) 开始往前遍历，找到第一个小于等于 \(a_{i+1}\) 的元素位置 \(j\)， 然后将 \(a_{i+1}\) 插入到位置 \(j+1\) 处。此时，序列 \(A[1,i+1]\) 就是已排序的。 因此，每次我们都是在上一次的最优解（即已排序子序列）的基础上获得一个新的元素，并求出新的最优解。 这就是一个典型的体现 动态规划（Dynamic Programming） 思想的递推求解过程。

显然，当序列中只有一个元素时，其必然是有序的，这就是递推的初始条件。

Insertion sort

图 4 Insertion sort
Swfung8, CC BY-SA 3.0
via Wikimedia Commons#

void insertion_sort(vector<int> &array, int left, int right) {
    for (int i = left + 1; i <= right; ++i) {  // array[left, i) has been sorted
        int key = array[i], j;                 // key is the element to be inserted
        for (j = i - 1; j >= left && array[j] > key; --j) {
            array[j + 1] = array[j];
        }
        array[j + 1] = key;
    }
}

void insertion_sort(vector<int> &array, int left, int right) {
    if (left >= right) return;

    insertion_sort(array, left, right - 1);  // array[left, right) has been sorted
    
    int key = array[right], j;               // key is the element to be inserted
    for (j = right - 1; j >= left && array[j] > key; --j) {
        array[j + 1] = array[j];
    }
    array[j + 1] = key;
}

Wikipedia Visualgo LeetCode 912

这是否是动态规划？#

注意我们这里的表述，插入排序只能说体现了动态规划的递推思想，但严格来说不能算作是一类动态规划算法。 动态规划的核心思想是将原问题分解为若干个 存在递推关系的 子问题，通过求解子问题的最优解，逐步推导出原问题的最优解。 在这个过程中，需要记录并重复利用子问题的解，以避免重复计算。具体地，动态规划需要满足三个要素：最优子结构、无后效性、重叠子问题。 而很显然插入排序的子问题并不是重叠的，因为每一次插入都对原先的有序数组进行了一次改动， 因此无法直接重复利用子问题的解，插入之前依旧需要进行多次的比较。

换而言之，如果我们采用递归写法，无法通过记忆化技术来优化插入排序的复杂度。

减而治之的核心思想是将原问题分解成若干个 相似的 子问题，在求解每个子问题的过程中，通过缩小问题规模来逐步得到大问题的解。 在这个过程中，每个小问题都是独立的。减而治之和动态规划的最大区别在于前者没有子问题的重叠和子问题的最优性这两个条件。

借助直观感受来比较，递推思想的初始子问题规模总是最小的，然后逐步扩大子问题规模，直到达到原问题的规模。 而减而治之则是从发现规模较大的平凡子问题开始，逐步缩小子问题规模，直到解决完所有子问题。

💡 使用动态规划求解斐波那契数列问题

斐波那契数列问题天然地适合使用动态规划的思想求解，因为它的子问题之间显式地存在着递推关系。 且可以重复利用子问题的解，既不用重复的计算，也不用额外的空间来记录所有的子问题的解。

由自顶而下递归，改为自底而上迭代：

def fibonacci_dp(n):
    f, g = 1, 0
    for _ in range(n):
        g = g + f
        f = g - f
    return g

Wikipedia LeetCode 912

时间复杂度为 \(O(n)\)，空间复杂度为 \(O(1)\).

注意

到目前为止，基于减而治之策略的排序算法的递归实现和基于递推思想的迭代实现各有特点， 似乎某一类的递归调用自身发生在解决平凡子问题前，另一类则发生在解决平凡子问题后。这绝非偶然。

在后面的小节我们将介绍快速排序和归并排序，它们的递归实现特点也十分明显。

参见

想一想，插入排序算法在寻找插入位置的过程中，我们是从后往前依次比较，直到找到合适的位置。 有没有更加高效的寻找插入位置的方法呢？感兴趣的读者可阅读对 二分查找算法 的介绍。

快速排序#

冒泡排序和选择排序都体现了减而治之的思想，但它们的效率都不高。 不难发现其中的一个重要因素是每次遍历处理后，都只能将原问题的规模减少一个单位。 我们是否可以通过一次遍历，将原问题的规模减少多个单位呢？更进一步地，能否尝试将问题规模减半呢？ 这引出了我们的另一种算法设计思想，分治（Divide-and-Conquer），又叫分而治之。

接下来，通过介绍 快速排序（Quicksort） 算法，我们将看到这是完全可行的。

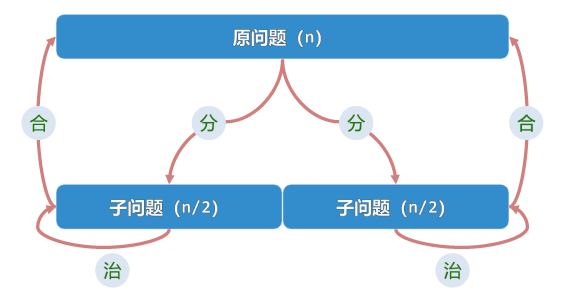
Divide-and-conquer

图 5 分而治之 （ via THUDSA [11] 配套讲义，对源文件有修改）#

分而治之的核心思想是：为求解一个大规模的问题，可以将其 划分 为若干子问题（通常两个，且规模大体相当）， 分别求解子问题，由子问题的解，合并得到原问题的解。 初步看上去，分而治之与减而治之的思想有些类似，但它们的区别在于分而治之的子问题之间是 相互独立 的， 这就意味着我们可以 并行 地求解子问题，从而提高算法的效率。 另外从缩减问题规模的角度来看，分而治之有着得天独厚的优势。

主定理（Master Theorem）

分治策略的时间复杂度递推式通常（但不总是）形如：

\[ T(n) = a * T(n/b) + O(f(n)) \]

表示原问题被划分成 \(a\) 个规模为 \(n/b\) 的子问题，\(f(n)\) 表示划分问题与合并解的步骤的时间复杂度。

💡 \(f(n)\) 复杂度对 \(T(n)\) 的影响

  • 若 \(f(n) = O(n^{\log _b a - \epsilon})\), \(\epsilon > 0\)，则 \(T(n) = \Theta(n^{\log _b a})\)

  • 若 \(f(n) = O(n^{\log _b a} \cdot \log ^k n), k \geq 0\)，则 \(T(n) = \Theta(n^{\log _b a} \cdot \log ^{k+1} n)\).

  • 若 \(f(n) = \Omega(n^{\log _b a + \epsilon})\), \(\epsilon > 0\)，且 \(a f(n/b) \leq c f(n)\)，\(c < 1\)，则 \(T(n) = \Theta(f(n))\).

简记方式，通常情况下 \(a\) 与 \(b\) 相等， 因此我们比较 \(f(n)\) 与 \(n\) 的关系来判断其最终对 \(T(n)\) 的影响程度：

  • 若 \(f(n) < n\), 则 \(T(n) = \Theta(n)\).

  • 若 \(f(n) = n\), 则 \(T(n) = \Theta(n \log n)\). （下式 \(k=0\) 的特例）

  • 若 \(f(n) = n \cdot \log ^k n, k \geq 1\), 则 \(T(n) = \Theta(n \log ^{k+1} n)\).

  • 若 \(f(n) >> n\), 则 \(T(n) = \Theta(f(n))\).

我们可以看到下面的两个排序算法，它们的时间复杂度都是 \(O(n \log n)\).

分而治之：自顶向下#

快速排序的核心思想

  1. 从待排序的数组中任选一个元素作为 基准（pivot）；

  2. 遍历并 分区（partition），将数组中所有小于基准的元素移动到左边，否则移动到右边；

  3. 对两边的子分区，重复步骤 1 和 2，直到子数组的长度为 1，此时子数组显然有序。

快速排序的子问题

如何选取 Pivot？采用何种分区策略？这会影响到算法性能，以及实现的复杂程度。

Quick sort

图 6 Quicksort
Matt Chan, CC BY-SA 3.0
via Wikimedia Commons#

void quick_sort(vector<int> &array, int left, int right) {
    if (left >= right) return;

    int i = left, j = right;  // two pointers
    int pivot = array[left + (right - left) / 2];  // select middle element as pivot
    while (i < j) {
        while (array[i] < pivot) i++;
        while (array[j] > pivot) j--;
        if (i <= j) swap(array[i++], array[j--]);
    } // note finally i > j

    quick_sort(array, left, j);   // left side of pivot
    quick_sort(array, i, right);  // right side of pivot
}

void quick_sort(vector<int> &array, int left, int right) {
    stack<pair<int, int>> stk;
    stk.push({ left, right });

    while (!stk.empty()) {
        auto [l, r] = stk.top(); stk.pop();
        if (l >= r) continue;

        int i = l, j = r, pivot = array[l + (r - l) / 2];
        while (i < j) {
            while (array[i] < pivot) i++;
            while (array[j] > pivot) j--;
            if (i <= j) { swap(array[i++], array[j--]); }
        }

        stk.push({ l, j });
        stk.push({ i, r });
    }
}

void quick_sort(vector<int> &array, int left, int right) {
    if (left >= right) return;

    int i = left, j = right;  // two pointers
    int pivot = array[left + rand() % (right - left)];
    while (i < j) {
        while (array[i] < pivot) i++;
        while (array[j] > pivot) j--;
        if (i <= j) swap(array[i++], array[j--]);
    } // note finally i > j

    quick_sort(array, left, j);   // left side of pivot
    quick_sort(array, i, right);  // right side of pivot
}

void quick_sort(vector<int> &array, int left, int right) {
    if (left >= right) return;
    
    int i = left, j = left, k = right;  // three pointers
    int pivot = array[left + (right - left) / 2];
    
    while (j <= k) {
        if (array[j] < pivot) swap(array[i++], array[j++]);
        else if (array[j] > pivot) swap(array[j], array[k--]);
        else j++;
    } // now array[left, i) < pivot, array(k, right] > pivot
    // array[i, j) == pivot, array[j, k] not exists (because j > k now)
    
    quick_sort(array, left, i - 1);   // left side of pivot
    quick_sort(array, k + 1, right);  // right side of pivot
}

Wikipedia Visualgo 1另外，Visualgo 给出的快速排序默认选用第一个元素作为 Pivot, 这依旧会导致最坏情况下的时间复杂度退化为 \(O(n^2)\). 因此，我们在这里采用了更为常见的选择中间元素作为 Pivot 的方法。 LeetCode 912 AcWing 785

💡 更好的 Pivot 选取策略：三中值

同每次都选取第一个元素作为 Pivot 一样，每次都选取最后一个元素作为 Pivot 也会导致最坏情况下的时间复杂度退化为 \(O(n^2)\). 即使每次都选取中间元素作为 Pivot，也无法避免最坏情况的出现（我们不难构造出这样的初始序列）。 根据 Sedgewick 的建议， 采用 “三中值” 法，即选取第一个元素、最后一个元素和中间元素的中间值作为 Pivot, 可以有效地避免最坏情况的出现。

💡 处理存在大量重复元素的情况：三路快排

如果我们选中了一个大量重复的元素作为 Pivot, 那么在排序的过程中，会出现大量的重复元素之间的交换，导致算法性能的下降。 为了处理这种情况，一种改进策略是在分区是采用 “三路快排”： 将当前的区间分为三部分，分别是小于 Pivot 的部分、等于 Pivot 的部分和大于 Pivot 的部分。 在后续递归处理时，只需要处理小于 Pivot 和大于 Pivot 的部分即可，而等于 Pivot 的部分则不需要再处理。 该改进已经在 qsort() 函数中实现， 读者可以查阅荷兰国旗问题（Dutch national flag problem）了解更多细节。

快速排序的时间复杂度分析

分区操作至多执行 \(\log n\) 次，即在至多 \(\log n\) 次内，问题规模将缩减为 \(1\), 退化成平凡情况。 每次分区需要在多个子区间遍历当前的所有元素，总体遍历数量仍旧是 \(n\), 因此时间复杂度为 \(O(n \log n)\).

请尝试根据递推关系式 \(T(n) = 2 \cdot T(n/2) + O(n)\) 推导出时间复杂度为 \(O(n \log n)\).

归并排序#

小技巧

再度回忆一下插入排序算法，其平凡子问题为：将一个元素插入到一个已经有序的序列中，且在问题规模为 0 时，问题退化至平凡。 我们可以将插入排序的思想推广到更一般的情况，即将两个已经有序的序列合并成一个有序的序列。 你可以理解成这个平凡子问题不再是每次将一个元素插入到一个有序序列中，而是 将一个有序序列插入到另一个有序序列中。

我们称之为归并（Merge），对应的算法叫做归并排序（Merge sort）。

分而治之：自底向上#

归并排序的核心思想

  1. 将一个序列分成两个子序列，分别对两个子序列进行归并排序（递归调用自身）；

  2. 当序列长度为 1 时，问题退化至平凡，单个元素无需排序；

  3. 子序列排序后，将两个有序的子序列合并成一个有序的序列；

如果你觉得递归的思想很难理解，那么我们可以先从自底向上的角度来理解归并排序。 借用《易经》中的概念：“易有太极，是生两仪，两仪生四象，四象生八卦。” 我们做的无非是两个长度为 1 的元素合并成一个长度为 2 的有序序列， 再将两个长度为 2 的有序序列合并成一个长度为 4 的有序序列，以此类推… 不断地通过解决两两合并这种平凡子问题，最终解决原始问题。

归并排序的子问题

如何合并两个有序序列？是否对空间占用有限制？

Merge sort

图 7 Merge sort
Swfung8, CC BY-SA 3.0
via Wikimedia Commons#

void merge_sort(vector<int> &array, int left, int right) {
    if (left >= right) return;

    int mid = left + (right - left) / 2;
    merge_sort(array, left, mid);
    merge_sort(array, mid + 1, right);

    // merge
    int i = left, j = mid + 1, k = 0;
    vector<int> tmp(right - left + 1);  // store the merged result temporarily
    while (i <= mid && j <= right) {
        if (array[i] <= array[j]) tmp[k++] = array[i++];
        else tmp[k++] = array[j++];
    }
    while (i <= mid) tmp[k++] = array[i++];
    while (j <= right) tmp[k++] = array[j++];

    // put back from tmp to array
    for (int i = left; i <= right; ++i)
        array[i] = tmp[i - left];
}

void merge_sort(vector<int>& array, int left, int right) {
    stack<pair<int, int>> stk, tmp;  // tmp is a helper stack
    tmp.push({ left, right });
    stk.push({ left, right });

    // handle the interval endpoints in advance to determine the order of merging
    while (!tmp.empty()) {
        auto [l, r] = tmp.top(); tmp.pop();
        if (l >= r) continue;
        
        int mid = l + (r - l) / 2;
        tmp.push({ l, mid });
        tmp.push({ mid + 1, r });
        stk.push({ l, mid });
        stk.push({ mid + 1, r });
    }
    
    while (!stk.empty()) {
        auto [l, r] = stk.top(); stk.pop();
        if (l >= r) continue;

        // merge
        int mid = l + (r - l) / 2;
        int i = l, j = mid + 1, k = 0;
        vector<int> tmp(r - l + 1); 
        while (i <= mid && j <= r) {
            if (array[i] <= array[j]) tmp[k++] = array[i++];
            else tmp[k++] = array[j++];
        }
        while (i <= mid) tmp[k++] = array[i++]; 
        while (j <= r) tmp[k++] = array[j++];

        // put back from tmp to array
        for (int i = l; i <= r; ++i) array[i] = tmp[i - l];
    }
}

此时不妨思考一下，为什么归并排序的迭代版实现，相较于快速排序的迭代版实现，多用了一个栈？ 你有办法优化空间复杂度吗？回想一下递归的不同实现，我们前面提到的尾递归形式有什么好处？

Wikipedia Visualgo LeetCode 912 AcWing 787

归并排序的时间复杂度分析

考虑当前有序元素数量，即在至多 \(\log n\) 次内，当前有序元素数量将从 \(1\) 变为 \(n\). 每次合并需要在多个子序列遍历当前的所有元素，总体遍历数量仍旧是 \(n\), 因此时间复杂度为 \(O(n \log n)\).

请尝试根据递推关系式 \(T(n) = 2 \cdot T(n/2) + O(n)\) 推导出时间复杂度为 \(O(n \log n)\).

算法设计没有不二法门#

迄今为止，我们初步接触了算法设计的几个基本策略：减治、分治、动态规划。

是否可以得出结论，一切分治策略就是最优的算法设计策略呢？答案是否定的。

不妨试试设计一个算法，解决如下问题：

最大区间和#

最大区间和问题（Maximum subarray problem）

输入：

一个长度为 \(n\) 的整数序列 \(A = \{a_1, a_2, \cdots, a_n\}\).

输出：

最大区间和，即找出 \(A\) 的一个连续子序列 \(A[i, j]\)，使得 \(\sum_{k=i}^j a_k\) 最大.

Wikipedia LeetCode 53

求数组 nums 在区间 [left, right] 内的最大区间和，记为 maxSubArray(nums, left, right).

小技巧

蛮力算法是最直接的思路，枚举所有的子序列计算其区间和，最终得到最大值，时间复杂度为 \(O(n^3)\). 倘若使用上一章节提到的前缀和技巧，则时间复杂度可降低至 \(O(n^2)\). 有无更优的做法？

采用分而治之的思想，令 mid 为原始区间中点，最终返回结果将会是以下三种情况的最大值：

  • 最大区间和所在的区间不包括原始区间中点，则必为以下二者情况取最大值：

    • maxSubArray(nums, left, mid - 1): 最大区间和在左半区间内（递归求解）；

    • maxSubArray(nums, mid + 1, right): 最大区间和在右半区间内（递归求解）；

  • 最大区间和所在的区间包括原始区间中点（或者说跨越原始间中点）：

    • 由于必取区间中点 mid, 此时目标 [i, j] 区间和将满足：

      \[ S[i..j] = S[i..mid] + S[mid..j] - \text{nums}[mid], \quad i \leq mid \leq j \]

    • 分别求解左右两区间终点 i 与 j, 使得 S[i..mid] 与 S[mid..j] 最大，即可得到最大区间和；

    • 问题退化为平凡：已知区间起点，求区间终点的最大区间和问题，平凡子问题的时间复杂度为 \(O(n)\).

int maxSubArray(vector<int>& nums, int left, int right) {
    if (left >= right) return nums[left];

    int mid = left + (right - left) / 2;
    int maxLeft = nums[mid], maxRight = nums[mid];
    int sumLeft = 0, sumRight = 0;
    for (int i = mid; i >= left; --i) {
        sumLeft += nums[i];
        maxLeft = max(maxLeft, sumLeft);
    }
    for (int i = mid; i <= right; ++i) {
        sumRight += nums[i];
        maxRight = max(maxRight, sumRight);
    }
    int maxInclude = maxLeft - nums[mid] + maxRight;
    int maxNotInclude = max(maxSubArray(nums, left, mid - 1), \
                            maxSubArray(nums, mid + 1, right));
    return max(maxInclude, maxNotInclude);
}

不难分析得出，此算法的时间复杂度为 \(O(n \log n)\), 空间复杂度为 \(O(\log n )\).

在求解区间和的过程中，如果有一段子区间总和为负值，那么它对包含其的区间的求和收益是负面的。

借助此特点，注意到如下性质：

  • 假定理想的总和最大区段为 nums[i, j], 若存在 最短 总和非正后缀 nums[suffix, right], 只可能有：

    • 理想的 nums[i, j] 为 nums[suffix, right] 的真后缀（区间构成真包含关系）;

    • 区间 [suffix, right] 与 [i, j] 区间不相交（交集为空），即 suffix > j；

  • 反证法：否则的话，此时的相交区间为 [suffix, j], 其为区间 [i, j] 的后缀；

    • 对于理想区间 [i, j]，要满足为最短性，则必有后缀和 S[suffix, j] 非负；

    • 而已知 S[suffix, right] 非正，根据和的关系，此时必有 S[j, right] 为负；

    • 而区间 [j, right] 短于区间 [suffix, right], 这与前提中的 最短 矛盾。

因此可以借助减而治之的思想，从尾部开始线性扫描，先求当前后缀内的最大和。 每当发现构成一个非正后缀时，就去掉这一部分的后缀（问题规模得以缩减，但注意 ans 可能已经更新过了）， 重新计算剩余区间的最大区间和，直到扫描完毕，即可得到整个区间的最大区间和。

int maxSubArray(vector<int>& nums, int left, int right) {
    int maxSum = INT_MIN, sum = 0;
    for (int i = 0; i < nums.size(); ++i) {
        sum += nums[i];
        maxSum = max(maxSum, sum);
        if (sum < 0) {
        sum = 0;
        }
    }
    return maxSum;
}

此算法的时间复杂度为 \(O(n)\), 空间复杂度为 \(O(1)\).

遍历序列，在遍历序列的过程中，找出以当前位置作为区间右端点的最大区间和：

  • 遍历过程中维护一个当前前缀和 curPreSum 与一个最小前缀和 minPreSum；

  • 以当前位置作为区间右端点的最大区间和为 curPreSum - minPreSum；

int maxSubArray(vector<int>& nums, int left, int right) {
    int curPreSum = 0, minPreSum = 0, maxSubSum = INT_MIN;
    for (auto num: nums) {
        curPreSum += num;
        maxSubSum = max(maxSubSum, curPreSum - minPreSum);
        minPreSum = min(minPreSum, curPreSum);
    }
    return maxSubSum;
}

此算法的时间复杂度为 \(O(n)\), 空间复杂度为 \(O(1)\) (并没有计算出整个前缀和数组)。

可以发现，即使是使用前缀和思想，也需要找到关键性质来降低问题的复杂度。

思路本质上与前缀和思想相同，在遍历序列的过程中，找出以当前位置作为区间右端点的最大区间和：

  • 递推约定：设 \(dp(i)\) 表示以第 \(i\) 个元素为结尾的最大区间和；

  • 初始状态： \(dp(0) = nums[0]\);

  • 转移方程： \(dp(i) = \max(dp(i-1) + nums[i], nums[i])\);

  • 最终结果： \(ans = \max\{dp(i)\}\).

int maxSubArray(vector<int>& nums, int left, int right) {
    vector<int> dp(nums.size());
    dp[0] = nums[0]; // inital value (might be negative)
    int maxSubSum = nums[0];
    for (int i = 1; i < nums.size(); ++i) {
        dp[i] = max(dp[i-1] + nums[i], nums[i]);
        maxSubSum = max(maxSubSum, dp[i]);
    }
    return maxSubSum;
}

时间复杂度为 \(O(n)\), 空间复杂度为 \(O(n)\). 接下来优化空间复杂度： 由于 \(dp(i)\) 只与 \(dp(i-1)\) 有关，因此可以用一个变量 dp 来维护并自我更新。 有没有发现这个与前缀和做法有着异曲同工之妙呢？

int maxSubArray(vector<int>& nums, int left, int right) {
    int dp = nums[0]; // inital value (might be negative)
    int maxSubSum = nums[0];
    for (int i = 1; i < nums.size(); ++i) {
        dp = max(dp + nums[i], nums[i]);
        maxSubSum = max(maxSubSum, dp);
    }
    return maxSubSum;
}

这一版代码虽然是从动态规划优化而来，但如果采用贪心的思想设计算法，也能直接写出同样的代码。 除了上面的代码，贪心思想还可以用来对减治思想的前缀和写法进行解释，关键在于贪心策略的制定。 古诗有云：“横看成岭侧成峰，远近高低各不同”，从不同的视角出发，同样的算法实现可以得到不同的解释。 我们将会在后面的章节专门介绍贪心思想，感兴趣的读者可以提前阅读。

采用分而治之思想，其实也能设计出时间复杂度为 \(O(n)\) 的算法。 但这可能要用到一些比较高级的数据结构，比如线段树，我们在这简单进行铺垫， 高级数据结构将在后面的章节进行讲解。

此问题用动态规划解决已经是非常高效的算法了，杀鸡无需用牛刀，最合适的就是最好的。

备注

请你思考一下，如果最终需要输出最大区间和的区间范围，应该如何修改代码实现？